Représentation énergétique des systèmes

La représentation des systèmes est un exercice d’abstraction complexe. Différents outils sont utilisables : diagramme synoptique, schéma (électrique, cinématiques, …), SysML, … Chaque outil met l’accent sur certains aspects du système, et tous ne permettent pas de représenter des interactions multiphysiques.

La représentation énergétique macroscopique (REM ou EMR en anglais) permet de représenter graphiquement les systèmes multiphysiques suivant l’angle des transferts de puissance. Cet outil a été développé dans les années 2000 par le laboratoire d’électrotechnique et d’électronique de puissance de Lille (L2EP) pour les systèmes électromécaniques [1]. L’extension à d’autres physiques est possible et fera l’objet d’articles futurs.

La REM est aujourd’hui enseignée à l’université de Lille mais aussi dans d’autres universités du monde francophone et non-francophone [2]. Les services de recherche de grandes entreprises de l’électromobilité (Stellantis, Siemens Mobility, …) commencent à l’utiliser pour faciliter le dialogue entre les équipes de spécialités différentes. L’utilisation de cet outil est donc en pleine expansion.

Principes fondateurs

Le formalisme REM repose sur un principe fondateur : la causalité des actions. L’objectif de cette partie est de présenter ce principe et comment la représentation énergétique macroscopique en découle.

Causalité

En physique comme en philosophie, la cause précède l’effet : c’est parce qu’une action est réalisée qu’une réaction est produite en retour. Cette notion est liée à celle du temps, nous ne pouvons pas revenir dans le passé car l’effet suit toujours la cause. Même si la mécanique quantique tente parfois de contredire cette réalité.

Le concept de cause exige absolument qu’un chose A soit telle qu’une autre B en dérive nécessairement et suivant une règle absolument universelle.

Kant, Critique de la raison pure

Approche physique

D’un point de vue mathématique, les effets sont l’intégrale des causes depuis l’origine de temps, comme le montre l’équation ci-dessous.

\(\mathrm{Effet}(t) = \mathrm{Effet}(0) + \int_0^t \mathrm{Cause} (\tau)~\mathrm{d}\tau\)

Cependant, la plupart des formulations des lois de la physique sont sous forme différentielles, c’est-à-dire qu’elle utilisent la notion de dérivée, à l’instar du principe fondamental de la dynamique (PFD). Il faut alors les intégrer pour faire apparaître la causalité : c’est la force qui crée le mouvement.

\(m\frac{\mathrm{d} v}{\mathrm{d} t}(t) = \sum F_{ext}(t)\)

Dès lors, on remarque que les fonctions d’effet sont toujours continues, là où les fonctions de cause peuvent ne pas l’être. Ainsi, d’après le PFD, la vitesse ne peut pas varier instantanément. D’un point de vue énergétique cela s’entend bien, puisque l’énergie cinétique s’exprime \(\frac{1}{2} mv^2\), faire varier la vitesse instantanément impliquerait d’apporter une puissance infinie pendant une durée infiniment courte. Les plus curieux auront ici reconnu la définition d’une impulsion de Dirac, mais, rappelons-le, les distributions sont des outils mathématiques qui n’ont pas de réalité physique.

Dualité Effort-Flux

Ainsi, on comprend bien qu’un échange d’énergie nécessite la présence simultanée d’une cause et d’un effet : une force sans mouvement ne travaille pas. Ces deux grandeurs peuvent se formaliser sous la forme d’un flux et d’un effort généralisés, sans présumer duquel est la cause ou l’effet. Les flux généralisés sont, entre autre : le courant électrique, la vitesse linéaire, la vitesse angulaire ou le débit volumique. Là où les efforts associés sont : la tension, la force, le couple, la pression. Les grandeurs ainsi construites forment des couples de variables dont le produit représente la puissance transmise d’un système à un autre. Ces notions fonctionnent très bien en électromécanique et en fluidique, l’extension à d’autres physiques comme la thermique ou la chimie peut être plus complexe, c’est pourquoi nous les étudierons ultérieurement.

Effort	Flux	Puissance
Tension \(u\)	Courant \(i\)	\(ui\)
Force \(\vec{F}\)	Vitesse \(\vec{v}\)	\(\vec{F}.\vec{v}\)
Couple \(C\)	Vitesse \(\Omega\)	\(C \Omega\)
Pression \(P\)	Débit \(D_v\)	\(PD_v\)
Gradient de température \(\Delta T\)	Flux entropique \(\frac{\mathrm{d}S}{\mathrm{d}t}\)	\(\Delta T \frac{\mathrm{d}S}{\mathrm{d}t}\)

Règles de représentation

Maintenant que l’esprit de la Représentation Énergétique Macroscopique est présenté, attardons nous sur le principe même de cette représentation, le cœur de cet article. Pour représenter un système la REM utilise quatre types de blocs, regroupés en deux catégories : fournisseur d’énergie et transformateur d’énergie. Les deux se distinguent aisément dans le cas où les pertes sont négligées : la somme des puissances qui arrivent à un transformateur d’énergie est nulle à tout instant, contrairement à un fournisseur d’énergie.

Dans la première catégorie, on retrouve les sources d’énergie et les accumulateurs d’énergie. La seconde catégorie regroupe les éléments de conversion et de couplage. L’interaction entre deux éléments est matérialisée par une paire de flèches de sens opposés, indiquant la grandeur imposée (la cause) et la grandeur subie (l’effet). Chaque bloc possède une ou plusieurs paires de connexions avec d’autres blocs.

Source d’énergie

Les sources d’énergie sont matérialisées par une ellipse verte. Le nom de la source peut être indiquée à l’intérieur de l’ellipse pour améliorer la compréhension. De part sa nature, une source impose une grandeur déterminée : une source de tension électrique impose une tension et subit un courant.

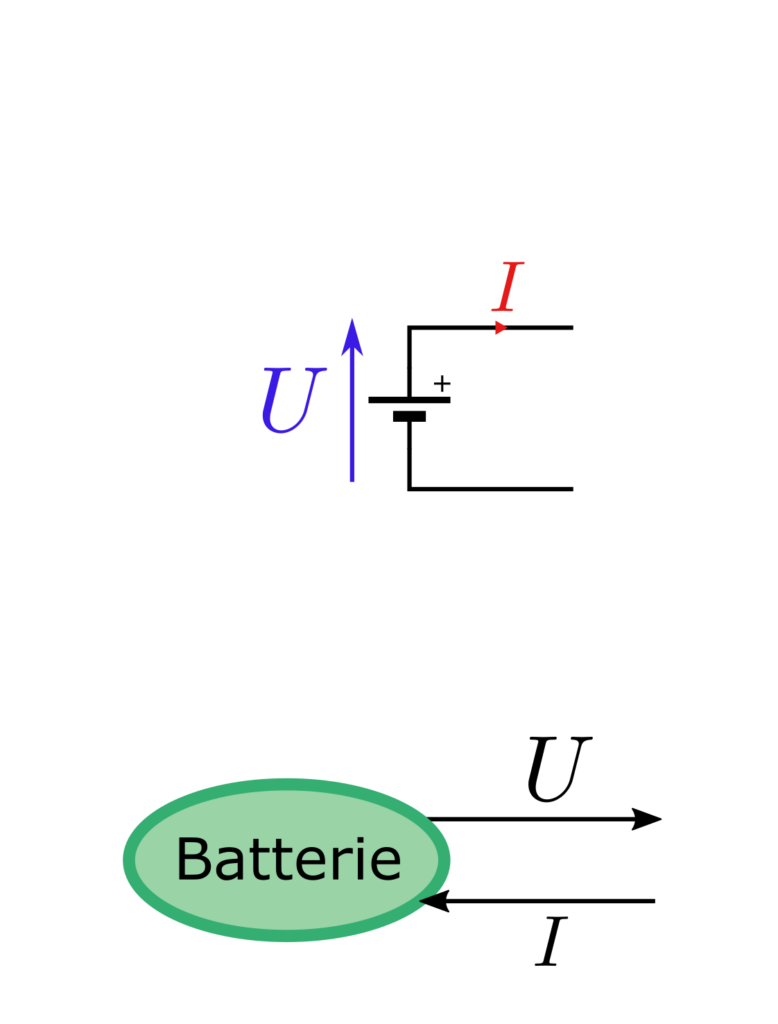
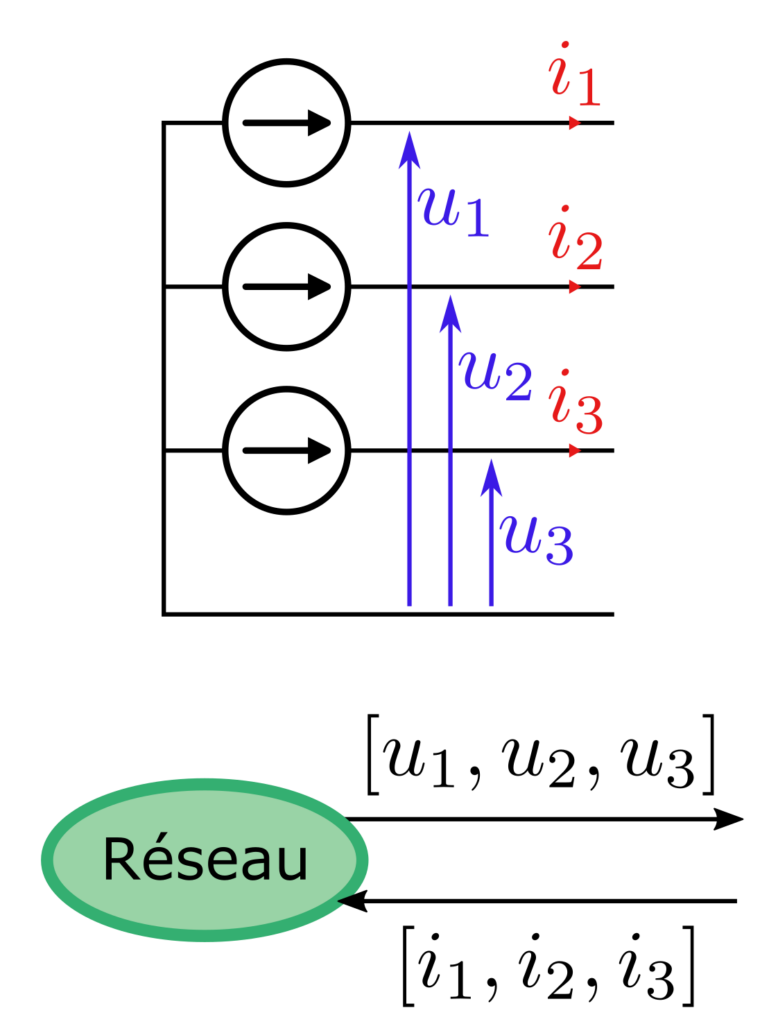
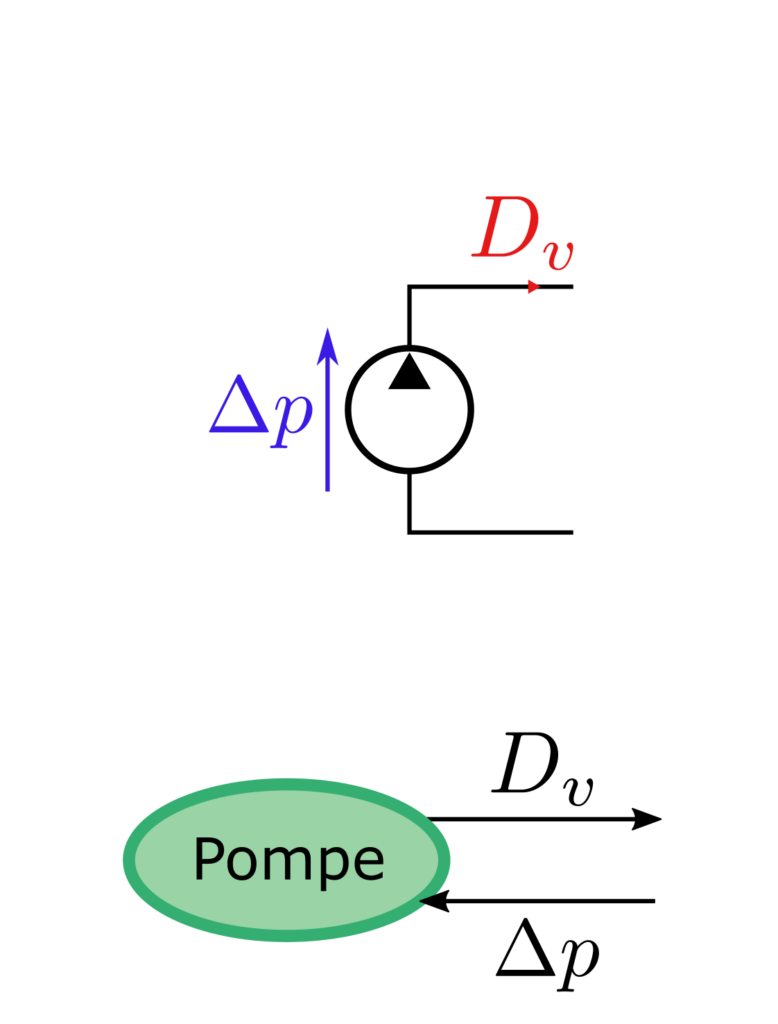
Ci-dessus, différentes sources d’énergie sont représentées. On remarque, sur l’exemple du réseau triphasé, que les grandeurs imposées et subies peuvent être vectorielles, voire matricielles ou tensorielles lorsque c’est pertinent. Seule contrainte dans ce cas : les vecteurs doivent avoir les mêmes dimensions. Ceci est dû au fait que l’utilisation de vecteurs masque en réalité l’existence de plusieurs entités REM : le réseau électrique triphasé peut être représenté par une source vectorielle ou trois sources scalaires.

Les grandeurs subies peuvent avoir un impact sur les grandeurs imposées. En effet, un générateur de tension non idéal verra sa tension de sortie \(U\) chuter lorsque le courant \(I\) qui le traverse augmente. De même, une pompe hydraulique verra sont débit \(D_v\) diminuer à mesure que la différence de pression \(\Delta p\) entre l’amont et l’aval augmente.

Les sources d’énergie sont très utiles pour modéliser un système mais n’ont en fait pas de réalité physique :

• une batterie est en fait un accumulateur (un stockage d’énergie),
• l’énergie du réseau électrique provient de différents centres de production de conversion d’énergie (voir cet article sur l’énergie dans le monde),
• une pompe à besoin d’énergie mécanique pour fonctionner.

Accumulateur d’énergie

Les accumulateurs d’énergie sont représentés par un rectangle rouge barré sur fond orange. Ces blocs représentent toutes les entités pouvant stocker, sous une forme ou une autre l’énergie. A l’instar des sources d’énergie, les accumulateurs définissent la grandeur qu’ils imposent : c’est dû à l’expression de la différentielle d’énergie pour ces systèmes. Ainsi, un condensateur impose une tension \(u\) car la variation de son énergie \(\mathrm{d} E = Cu\mathrm{d}u\) dépend de \(\mathrm{d}u\).

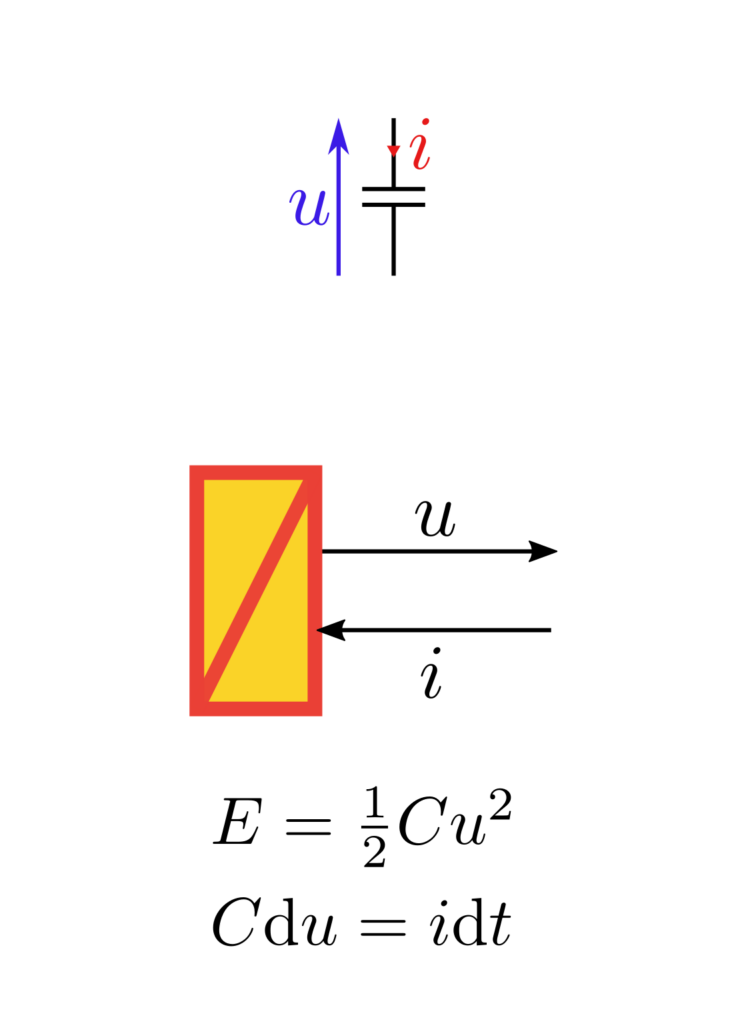
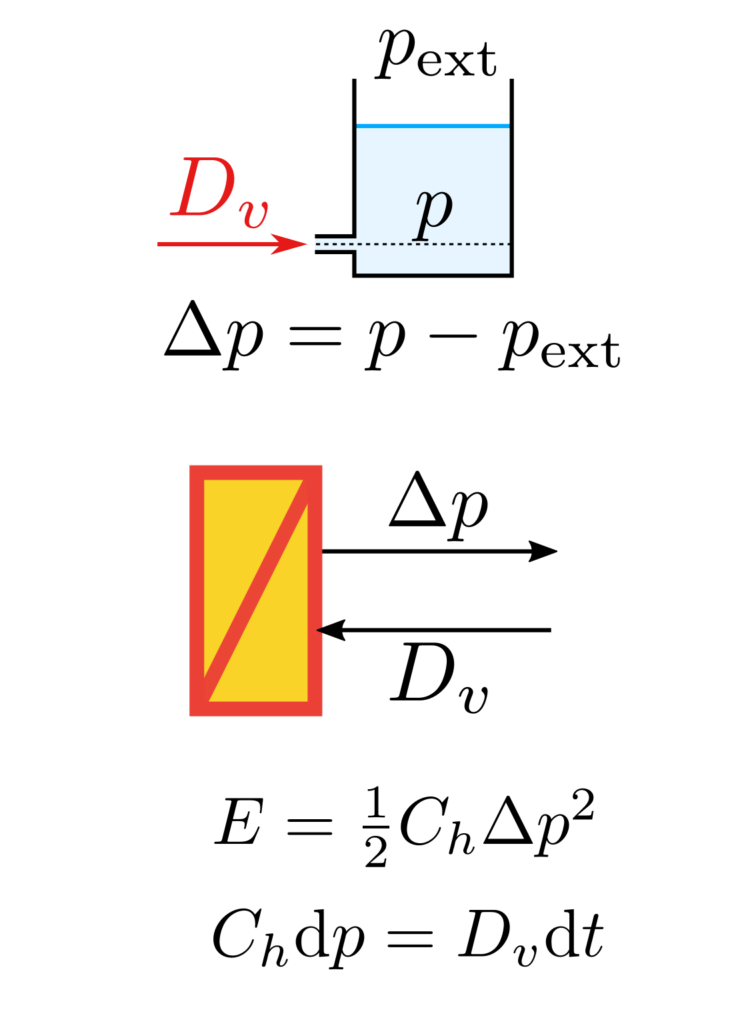
Ci-dessus, différents accumulateurs d’énergie sont représentés, dans différents domaines physiques : électrocinétique, mécanique newtonienne, mécanique des fluides. Dans les trois cas présentés, l’équation différentielle régissant le système est de la même forme. On distingue alors aisément le terme de cause (multiplié par \(\mathrm{d}t\) dans le membre de droite) et celui d’effet (différentielle dans le membre de gauche).

Une distinction peut être faite entre les accumulateurs de flux, comme une masse ou une inductance, et les accumulateurs d’effort, comme un condensateur ou un réservoir à liquide. L’énergie stockée dans les premiers peut être qualifiée d’énergie inertielle, à l’instar de l’énergie cinétique. Alors que l’énergie stockée dans les accumulateur peut être qualifiée d’énergie potentielle, à l’image de la hauteur d’eau d’un barrage.

De part leur statut de fournisseurs d’énergie, les sources et les accumulateurs définissent la grandeur qu’ils imposent, ce n’est pas le cas des transformateurs d’énergie que nous allons voir juste après.

Élément de conversion

Les éléments de conversions modifient la forme de l’énergie. Ils sont représentés par un carré rouge sur fond orange si la conversion est monophysique ou un cercle rouge sur fond orange si la conversion est multiphysique. Ils peuvent modifier la répartition entre effort et flux mais aussi la nature du couple effort-flux.

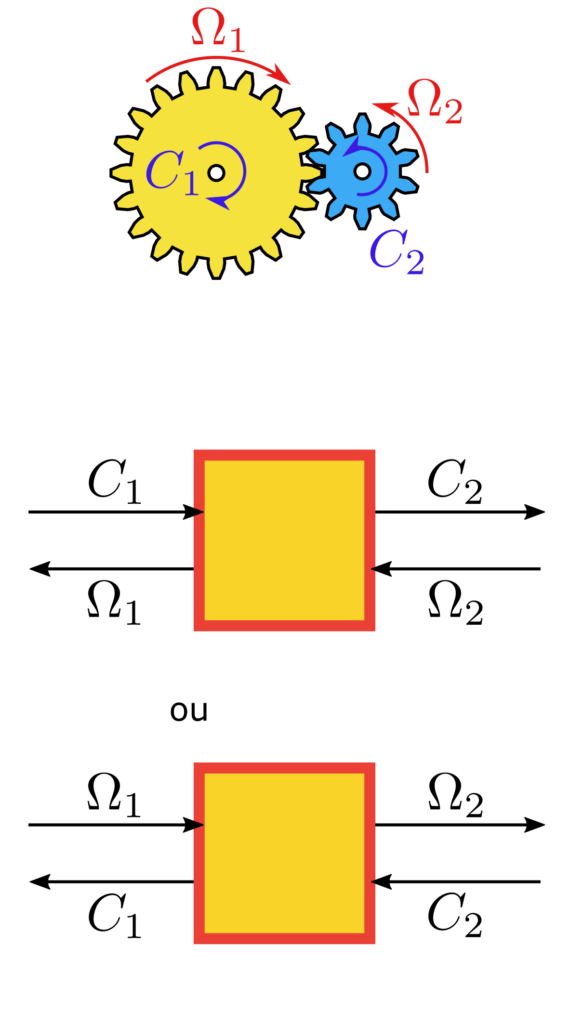
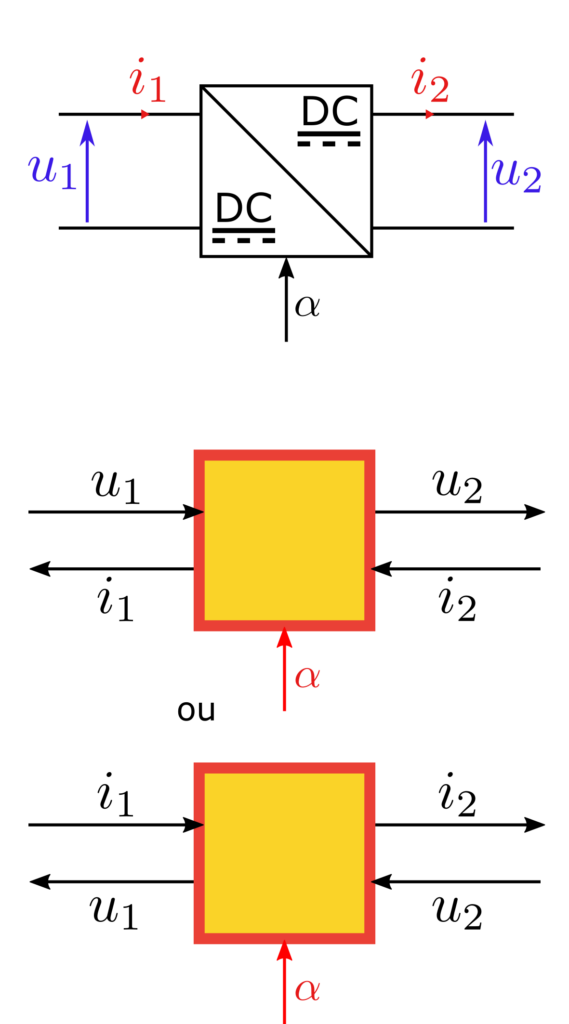
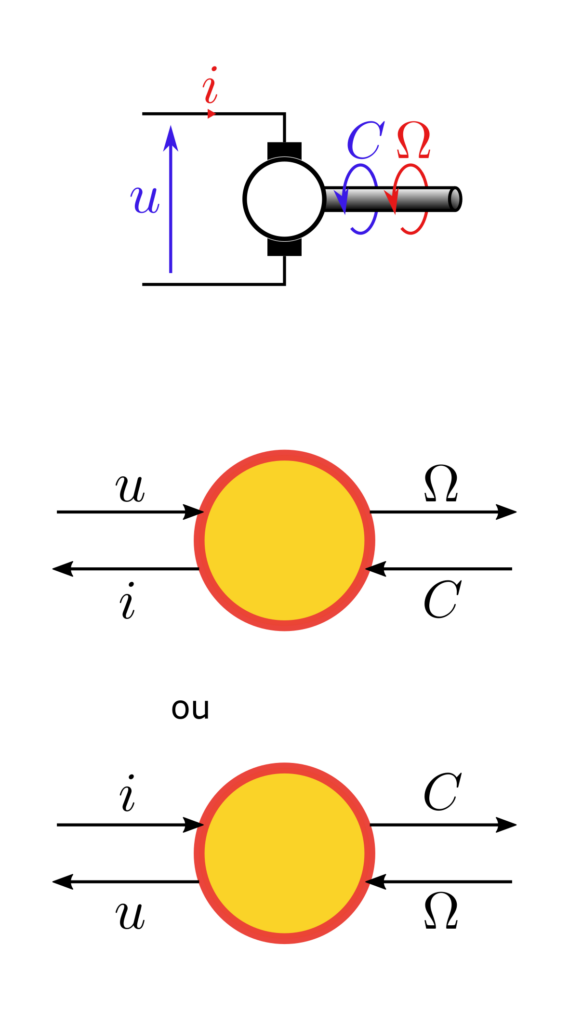
Les exemples ci-dessus illustrent la Représentation Énergétique Macroscopique d’applications de différents domaines de la physique. Comme dit précédemment, un élément de conversion ne définit pas les grandeurs qu’il impose. Ainsi, deux configurations sont possible pour chaque élément de conversion. C’est l’association de ce bloc, de manière directe ou indirecte, avec des fournisseurs d’énergie qui définit la configuration choisie.

Le convertisseur DC/DC réglable comporte une entrée par le dessous du bloc, c’est le paramètre de réglage du rapport cyclique \(\alpha\). Cette possibilité permet de définir des systèmes dynamiques et ouvre la porte au contrôle du système. Le contrôle de système complexe par inversion de modèle est intégré à la REM et fera l’objet d’un article ultérieur.

Élément de couplage

Enfin, la dernière catégorie d’élément en Représentation Énergétique Macroscopique est l’élément de couplage. Cet élément est représenté par deux symboles d’élément de conversion imbriqués, avec toujours une distinction entre mono et multiphysique. Ces éléments servent à représenter la répartition du flux de puissance entre différents chemins.

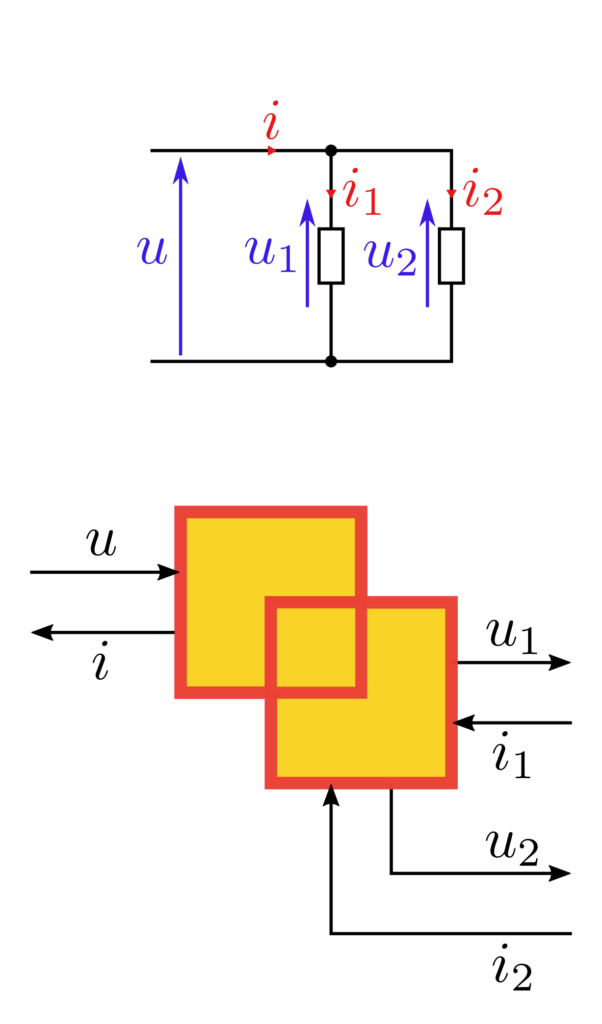
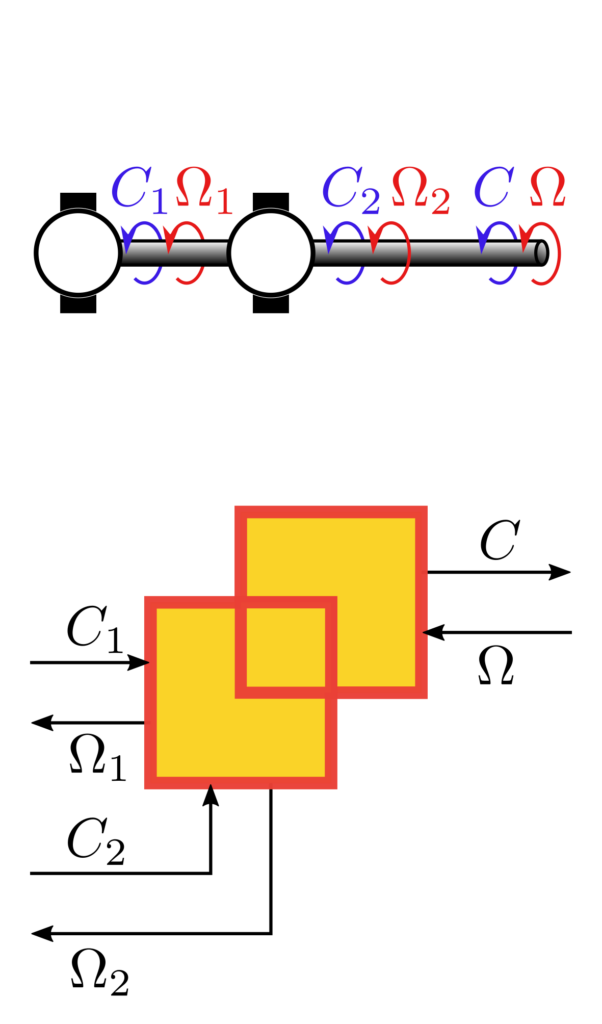
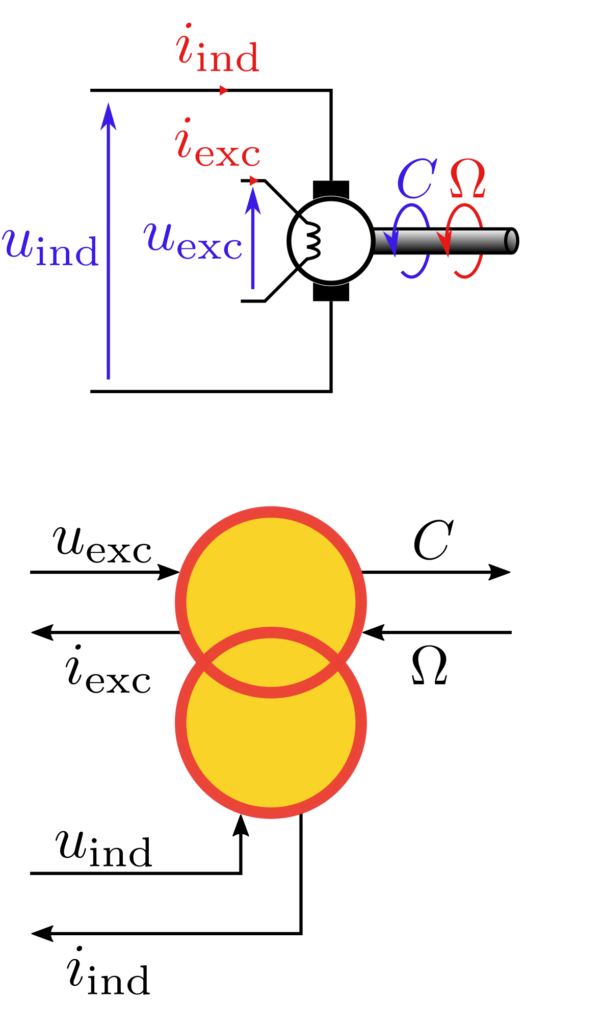
Les exemples ci-dessus illustrent différents couplages possibles. Les deux premiers représentent des lois fondamentales : la mise en commun de la tension et l’addition des courants lors d’une mise en parallèle électrique, et la mise en commun de la vitesse et l’addition des couples pour un arbre de transmission. Le troisième représente une MCC où l’excitation est séparée de l’inducteur. Dans cette dernière configuration, on comprend bien la nécessité de représenter trois flux d’énergie (inducteur, excitation et axe) dans deux domaines physiques différents (électrocinétique et mécanique).

Parfois, les accumulateurs sont représentés avec plusieurs paires d’entrée/sortie, c’est une simplification. Les accumulateurs fixant une grandeur, ils sont souvent utilisés pour distribuer cette grandeur à différents éléments. C’est pourquoi, lorsqu’un accumulateurs est représenté avec plusieurs paires d’entrée/sortie, il faut comprendre que c’est un accumulateur associé à un élément de couplage implicite.

Exemples de représentations

Tout l’intérêt de la REM est de représenter des systèmes complexes, et par la suite de les commander. Cette partie présente des exemples de représentation de systèmes relativement complexes.

Véhicule hybride

Les véhicules hybrides, en particulier thermique-électrique, sont dans l’air du temps. Ces systèmes sont pourtant complexes car ils comportent au moins deux sources de puissance mécanique : un moteur à combustion interne (MCI) et un groupe électromoteur (GEM). Le MCI est représenté par une source d’énergie car la conversion d’énergie (chimique vers mécanique) est difficile à représenter. Le GEM est composé d’une machine électrique associé à de l’électronique de puissance et un réducteur mécanique. Ce dernier est réversible en puissance, contrairement au MCI : on peut recharger la batterie au freinage. Les freins mécaniques n’ont volontairement pas été représentés.

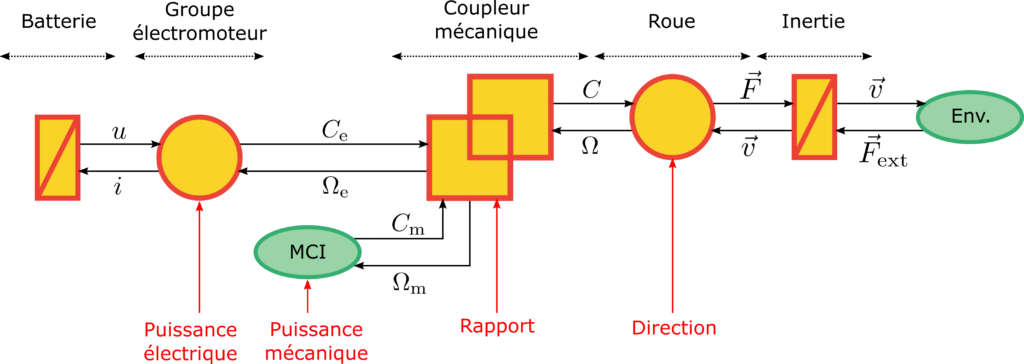
A travers cette représentation, les éléments important du véhicule sont mis en lumière, ainsi que les paramètres de réglage. En particulier, un conducteur veut pouvoir agir sur deux paramètres : la vitesse et la direction. Alors que le système comporte au moins quatre entrées de réglage : la direction des roues, le ou les rapports du coupleur mécanique qui fait office de boîte de vitesse (la clio V e-tech comporte des rapports pour le GEM et d’autres pour le MCI, soit deux paramètres), et enfin les consignes en puissance du MCI et du GEM.

On comprend alors l’enjeu en terme de contrôle que constituent de tels véhicules. Des stratégies de commande complexes sont nécessaires pour optimiser les flux de puissance en fonction des situations : MCI ou GEM seul, recharge de la batterie par le MCI, MCI et GEM ensemble… La force de la REM est de présenter de manière claire les flux de puissance et les commandes possibles.

Convertisseur DC/DC élévateur de tension

Le second cas étudié ici est celui d’un convertisseur Boost, qui permet de transformer une tension continue en une autre tension continue de valeur plus importante. C’est un cas d’étude classique de l’électronique de puissance.

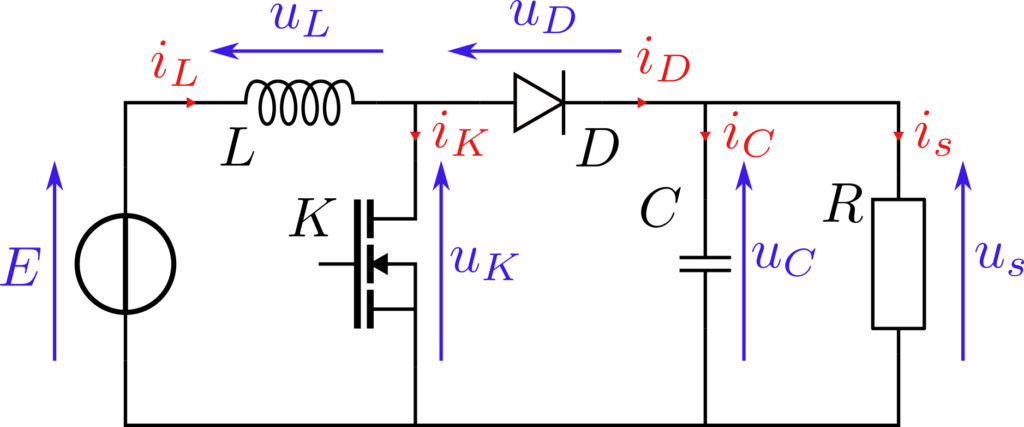
La représentation énergétique ci-dessous découle directement du schéma ci-dessus. On retrouve les éléments constitutif du circuit ainsi que leur rôle. L’inductance \(L\) impose le courant d’entrée et le condensateur \(C\) impose la tension de sortie. Le bloc de conversion représente la cellule de commutation qui subit les grandeurs précédentes et impose la tension aux bornes de l’interrupteur et le courant dans la diode.

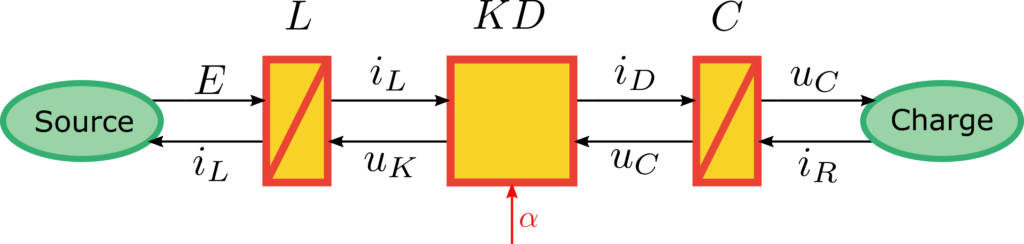
Le paramètre de réglage \(\alpha\) est mis en évidence. La mise en équation du système permet d’obtenir les équations suivantes :

Inductance \(L\)	\(i_L = \frac{1}{L} \int \left( E-u_K \right) \mathrm{d} t\)
Condensateur \(C\)	\(u_C = \frac{1}{C} \int \left( i_D-i_R \right) \mathrm{d} t\)
Transistor \(K\)	\(u_K = \alpha u_C\)
Diode \(D\)	\(i_D = \alpha i_L\)
Charge \(R\)	\(i_R = \frac{u_C}{R}\)

Ces équations peuvent ensuite facilement être implémentées dans un outil de simulation, comme MatLab/Simulink, pour étudier le comportement du système. La modélisation étant causale, la simulation est plus rapide qu’une simulation du circuit par une méthode acausale.

Application à la modélisation des systèmes

La REM n’est pas une modélisation mais, comme son nom l’indique, une représentation. Cela veut dire elle ne présage pas du niveau de modélisation de chaque sous système. Elle représente les sous-systèmes d’après leur rôle dans le système mais pas d’après leur modèle. Les choix fait pour représenter le système global en différents éléments résulte cependant d’une modélisation du système dans son ensemble.

Ainsi la REM peut être vue comme un outil pour la modélisation, en découpant un système complexe en plusieurs sous-systèmes simples et facilement modélisables. MatLab/Simulink est un bon environnement pour réaliser des simulations en utilisant la REM, vous pouvez trouver une bibliothèque ici.

Pluralité des niveaux de modélisation

En fonction des besoins, on peut choisir un modèle plus ou moins fin pour les éléments d’un système. Dans un premier temps, pour comprendre le fonctionnement d’un convertisseur Boost, on choisira des composants idéaux (comme précédemment) et on replacera le rapport cyclique \(\alpha\) par une fonction de modulation \(f_m\) donnant l’état de l’interrupteur \(K\). Si maintenant on veut réguler ce même convertisseur, un modèle moyen peut dans un premier temps suffire. Dans le cas d’une étude de rendement, il sera alors intéressant de prendre en compte les pertes dans les éléments actifs et passifs. Enfin, dans le cas d’une étude CEM, un modèle fin des composants passifs doit être pris en compte, ainsi que la dynamique de commutation des interrupteurs.

Ainsi, La représentation du système reste identique mais le contenu des éléments varie en fonction des besoins, c’est une force de la REM. Ce système a été mis en place lors du projet européen PANDA (Powerful Advanced N-Level Digital Architecture for models of electrified vehicles and their components) [3] initié par le L2EP de Lille. Dans ce projet, une bibliothèque pour Simcenter AMESIM a été développée afin de partager les modélisations entre les partenaires industriels et académiques. Plusieurs niveaux de modélisations ont été incorporés avec la possibilité pour les industriels de réaliser des modèles boîte noire afin de conserver leur connaissance.

Sources

• [1] Projet EMR de l’université de Lille, site officiel du formalisme REM, https://emr-website.univ-lille.fr/
• [2] La REM, formalisme multiphysique de commande de systèmes énergétiques, Techniques de l’ingénieur, D3066
• [3] Panda project, site officiel du projet européen PANDA, https://project-panda.eu/

Toutes les figures de cette article sont de création personnelle et sont protégée par une licence CC-BY-NC. Vous pouvez les partager et les modifier tant que vous citez l’auteur et que l’utilisation n’est pas commerciale.

Image de couverture : Maggie Bartlett, National Human Genome Research Institute, Public domain, via Wikimedia Commons